一、什么是复杂度分析

1、定义

复杂度分析是计算机科学中用来衡量算法在最坏情况下运行时间或空间需求的一种方法。这种估算方法被称为渐近复杂度分析（asymptotic complexity analysis），简称复杂度分析。

  • 时间效率：算法运行时间的长短。
  • 空间效率：算法占用内存空间的大小。

2、基本概念

（1)时间复杂度：算法执行所需时间随输入数据大小增长的变化趋势。通常用大O表示法（O-notation）来描述。例如：

  • O(1)：常数时间复杂度，表示算法执行时间与输入数据大小无关。
  • O(n)：线性时间复杂度，表示算法执行时间与输入数据大小成正比。
  • O(n^2)：平方时间复杂度，表示算法执行时间与输入数据大小的平方成正比。
  • O(log n)：对数时间复杂度，表示算法执行时间与输入数据的对数成正比。

(2)空间复杂度：算法执行过程中所需的最大存储空间量，通常也用大O表示法来描述。例如：

  • O(1)：常数空间复杂度，表示算法使用的空间与输入数据大小无关。
  • O(n)：线性空间复杂度，表示算法使用的空间与输入数据大小成正比。

复杂度分析能够体现算法运行所需的时间和空间资源与输入数据大小之间的关系。它描述了随着输入数据大小的增加，算法执行所需时间和空间的增长趋势。

3、总结

  • “时间和空间资源”分别对应时间复杂度（time complexity）和空间复杂度（space complexity）。
  • “随着输入数据大小的增加”意味着复杂度反映了算法运行效率与输入数据体量之间的关系。
  • “时间和空间的增长趋势”表示复杂度分析关注的不是运行时间或占用空间的具体值，而是时间或空间增长的“快慢”。

4、作用

复杂度分析克服了实际测试方法的弊端，体现在以下几个方面。

  • 它无需实际运行代码，更加绿色节能。
  • 它独立于测试环境，分析结果适用于所有运行平台。
  • 它可以体现不同数据量下的算法效率，尤其是在大数据量下的算法性能。

一、 迭代与递归

在程序中实现重复执行任务，即两种基本的程序控制结构：迭代、递归。

1、迭代

迭代（iteration）是一种重复执行某个任务的控制结构。在迭代中，程序会在满足一定的条件下重复执行某段代码，直到这个条件不再满足

1.1、for循环

for 循环是最常见的迭代形式之一，适合在预先知道迭代次数时使用

以下函数基于 for 循环实现了求和 1+2+⋯+n，求和结果使用变量 res 记录

1
2
3
4
5
6
7
8
9
/* for 循环 */
int forLoop(int n) {
    int res = 0;
    // 循环求和 1, 2, ..., n-1, n
    for (int i = 1; i <= n; i++) {
        res += i;
    }
    return res;
}

此求和函数的操作数量与输入数据大小 � 成正比，或者说成“线性关系”。实际上，时间复杂度描述的就是这个“线性关系”。

流程框图

2、while循环

和for 循环类似，while 循环也是一种实现迭代的方法。在 while 循环中，程序每轮都会先检查条件，如果条件为真，则继续执行，否则就结束循环。

以下函数基于 while 循环实现了求和 1+2+⋯+n，求和结果使用变量 res 记录

1
2
3
4
5
6
7
8
9
10
11
/* while 循环 */
int whileLoop(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 2, ..., n-1, n
    while (i <= n) {
        res += i;
        i++; // 更新条件变量
    }
    return res;
}

while 循环比 for 循环的自由度更高。在 while 循环中，我们可以自由地设计条件变量的初始化和更新步骤。

例如在以下代码中，条件变量 � 每轮进行两次更新，这种情况就不太方便用 for 循环实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
/* while 循环（两次更新） */
int whileLoopII(int n) {
    int res = 0;
    int i = 1; // 初始化条件变量
    // 循环求和 1, 4, 10, ...
    while (i <= n) {
        res += i;
        // 更新条件变量
        i++;
        i *= 2;
    }
    return res;
}

总的来说，**for 循环的代码更加紧凑，while 循环更加灵活**，两者都可以实现迭代结构。选择使用哪一个应该根据特定问题的需求来决定。

3、嵌套循环

我们可以在一个循环结构内嵌套另一个循环结构，下面以 for 循环为例：

1
2
3
4
5
6
7
8
9
10
11
12
/* 双层 for 循环 */
String nestedForLoop(int n) {
    StringBuilder res = new StringBuilder();
    // 循环 i = 1, 2, ..., n-1, n
    for (int i = 1; i <= n; i++) {
        // 循环 j = 1, 2, ..., n-1, n
        for (int j = 1; j <= n; j++) {
            res.append("(" + i + ", " + j + "), ");
        }
    }
    return res.toString();
}

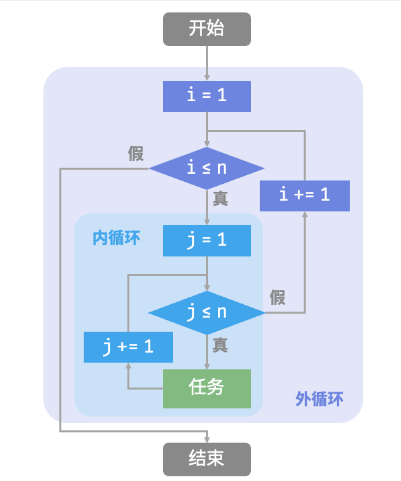
在这种情况下，函数的操作数量与 n^2^，或者说算法运行时间和输入数据大小 n 成“平方关系”。

我们可以继续添加嵌套循环，每一次嵌套都是一次“升维”，将会使时间复杂度提高至“立方关系”“四次方关系”，以此类推。

二、递归

递归（recursion）是一种算法策略，通过函数调用自身来解决问题。它主要包含两个阶段。

递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。

归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

1、递归的三要素

  1. 终止条件：用于决定什么时候由“递”转“归”。
  2. 递归调用：对应“递”，函数调用自身，通常输入更小或更简化的参数。
  3. 返回结果：对应“归”，将当前递归层级的结果返回至上一层。
1
2
3
4
5
6
7
8
9
10
/* 递归 */
int recur(int n) {
    // 终止条件
    if (n == 1)
        return 1;
    // 递：递归调用
    int res = recur(n - 1);
    // 归：返回结果
    return n + res;
}

三、递归迭代的对比

迭代 递归
实现方式 循环结构 函数调用自身
时间效率 效率通常较高，无函数调用开销 每次函数调用都会产生开销
内存使用 通常使用固定大小的内存空间 累积函数调用可能使用大量的栈帧空间
适用问题 适用于简单循环任务，代码直观、可读性好 适用于子问题分解，如树、图、分治、回溯等，代码结构简洁、清晰